In order to generate usable heat or electricity, a fusion generator requires fuel.  Currently, isotopes of hydrogen are the typical fuel of choice, although some other options are available.  For the nuclei of two atoms to fuse, they must collide with a high relative velocity.  High velocities imply high kinetic energies which imply high temperatures, such that “energetic” and “hot” tend to be used interchangeably.  At temperatures where fusion begins to occur, the fuel is hot enough that it has ionized and become a plasma.

Even if the fuel is hot enough for fusion events to be possible, fusion is still a statistical process.  For each collision that results in fusion, many collisions occur that have no effect beyond the nuclei bumping into each other.  In current experiments, about 1000 collisions occur for each fusion event.  Therefore, not only must the fuel be hot but it must also remain confined long enough for a sufficient number of collisions to occur.  We must somehow counteract the hot fuel’s natural tendency to expand.

More collisions occur in a denser plasma since more nuclei are available to collide.  However, a denser plasma is more difficult to heat and also more difficult to confine.

The above three factors (temperature, density and duration of confinement), together known as the “triple-product”, form a measure of how successful a particular fusion generator can be.  As seen in the graph below, the highest attained value for the triple-product has increased at a faster rate than has the popular Moore’s Law, with the triple-product doubling every 1.8 years as compared to the 2 year doubling rate of the number of transistors on a chip.

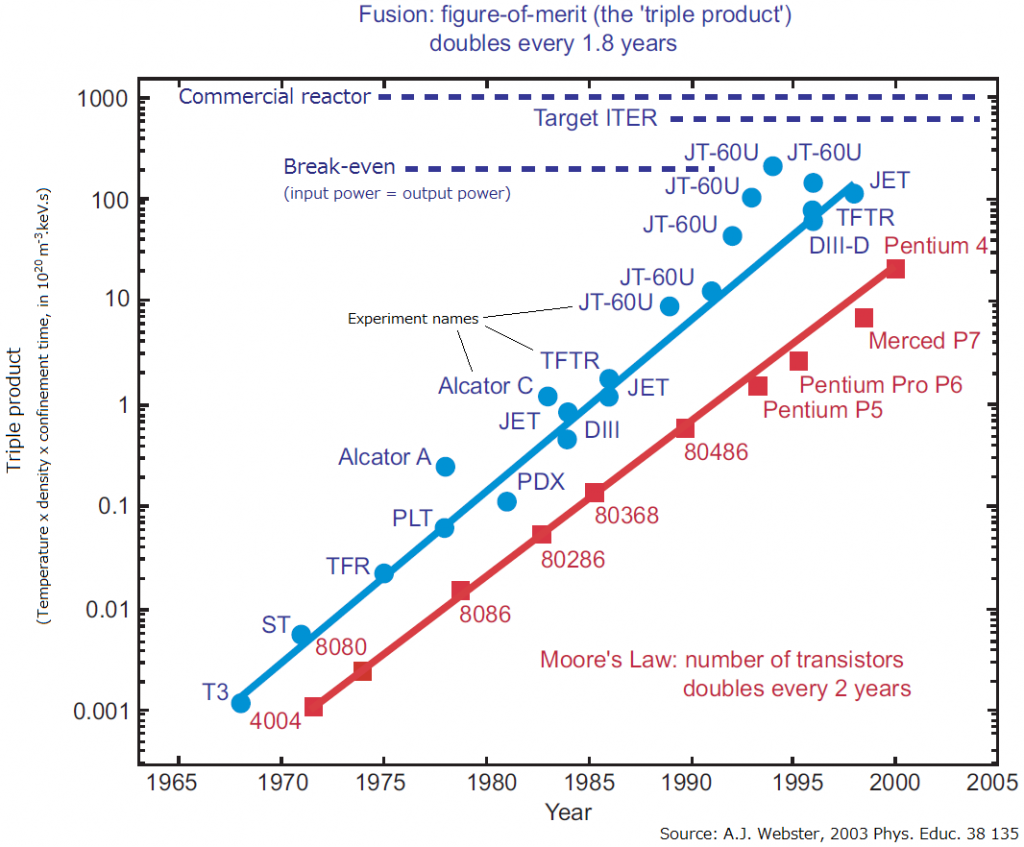
The big difference between Moore’s Law and the triple-product trend is that a small number of transistors can already be useful but fusion does not become useful until the break-even threshold is reached.  Only once the amount of energy released exceeds the amount of energy required to heat and confine the plasma initially does fusion become more than an academic interest.

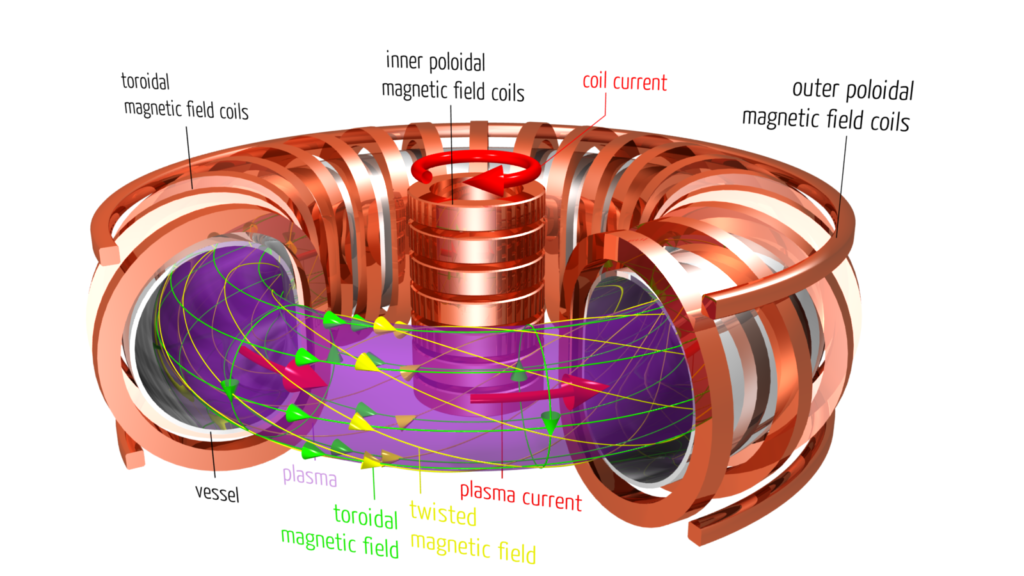
We are now well beyond the edge of the graph.  If we extrapolate, we should already have a commercial reactor, which is not the case.  One current issue that is slowing progress involves the interactions of the plasma with the physical walls of its container.  We attempt to keep the plasma with a container made of magnetic fields.  However, the magnetic container leaks.  The magnetic container is maintained inside a vacuum and the vacuum container has physical walls.  The plasma that leaks from the magnetic container hits the physical walls and generally undesirable things happen.  However, until recently, the physical walls had not been considered in the modeling of fusion generators.  The simplifications that had been used in order to deal with the complexity of the confined plasma resulted in the collisions with the physical walls being an insignificant contribution to the models.  In fact, even collisions within the plasma itself have often been ignored.  However, we have now reached the point that our models cannot improve further unless the interactions with the physical walls are taken into account.

My current research involves implementing a Monte Carlo collision operator to interface with an HPC-aware Particle-in-Cell code in order to perform plasma modeling that takes into consideration collisions both with the container walls and within the plasma.