Classical continuum models are often insufficient to predict the complex phenomena that emerge in the problems described above due their inherent multiscale nature. On the other hand, mesoscale and atomistic models have the potential to predict such phenomena, but often cannot extend into experimentally measurable spatial and temporal scales. Therefore, the material involved is modeled using a combination of a coarse scale model and a fine scale model. This modeling paradigm which is commonly referred to as multiscale modeling is playing an increasingly important role in scientific and industrial applications. The central theme of my research to date is to understand the link between the existing hierarchy of models, which is a precursor to developing robust multiscale methods.
Interface dislocations and grain boundary disconnections using Smith normal bicrystallography [Link]
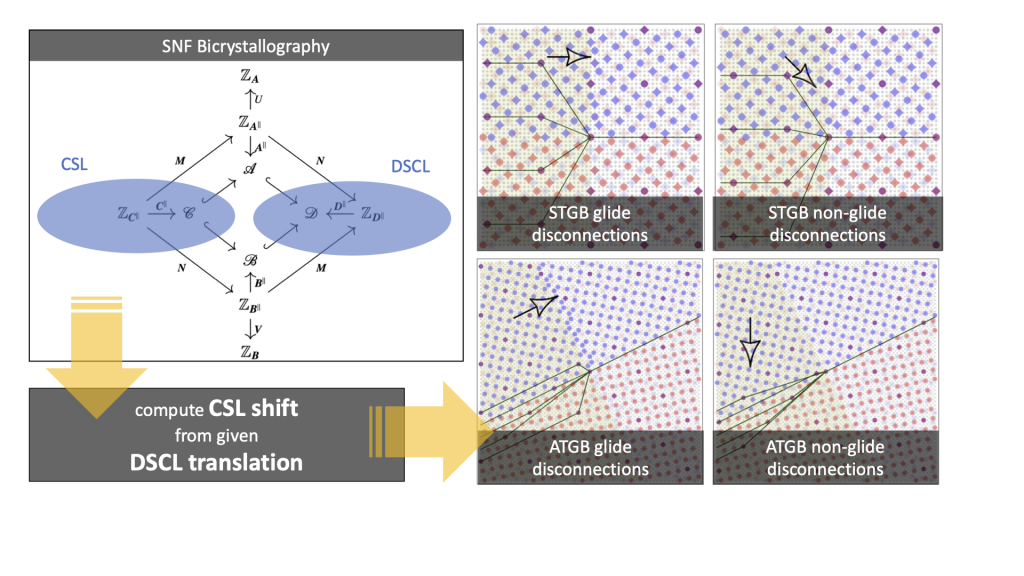
The CSL/DSCL model for interfaces in crystalline materials offers a unified framework to study interface dislocation in phase boundaries and disconnections in grain boundaries. The model relies on the existence of a coincidence relation between the two lattices that meet at an interface. The model’s ability to quantitatively predict the thermodynamics and kinetics of interfaces has been demonstrated for a limited set of symmetric tilt grain boundaries (STGBs) in cubic materials and twin boundaries. However, the lack of a general framework of interface defects prevents its applicability to arbitrary rational boundaries. In this paper, we present a mathematical framework based on the Smith normal form (SNF) for integer matrices to study the bicrystallography of rational phase and grain boundaries. One of the main results of the paper is constructive proof of the invariance of the coincident site lattice (CSL) under discrete relative displacements of the parent lattices (of a possibly different kind) by a displacement shift complete lattice (DSCL) vector. In addition, we obtain necessary and sufficient conditions on two lattices, related by not only rotations but also lattice distortions, for the existence of a coincidence relation.
We first apply these results to explore coincidence relations in arbitrary phase boundaries, and study interface dislocations. In particular, we demonstrate the framework for a phase boundary formed by a strained hexagonal lattice and a square lattice. As a second application, we show how to enumerate all possible (geometric) disconnection modes in arbitrary rational grain boundaries, including glide and non-glide modes in both STGBs and asymmetric-tilt grain boundaries (ATGBs). The constructive nature of the framework lends itself to an algorithmic implementation based exclusively on integer matrix algebra to construct all interfaces that admit CSLs up to a prescribed size, and determine disconnection modes in grain boundaries. We demonstrate the use of SNF bicrystallography on selected bicrystal misorientation axes/angles in face-centered cubic (fcc), body-centered cubic (bcc), and hexagonal (hex) lattices.
Interface mechanics of 2D materials on metal substrates [Link]
 |  |  |  | |
|---|---|---|---|---|
 |  |  |  | |
Experiment | Simulation time ----------> |
The chemical vapor deposition (CVD) of graphene on metal substrate serves as a robust method tosynthesize high quality graphene flakes. Therefore, understanding the thermodynamics and kineticsof graphene-metal interface is an important step towards synthesizing high quality graphene duringCVD. The focus of this paper is on the phenomenon of surface reconstruction of a metal substrateduring the deposition of a 2D material. Key features of surface reconstruction include the formationof straight and pyramidal facets of size∼100 nmin width and∼10 nmin height. In addition,discontinuities in facet directions under a single graphene flake distributed over two grains highlightthe strong crystallographic influence on surface reconstruction.In this paper, we present an atomistically informed continuum model of a graphene-metal in-terface in three dimensions. Graphene is modeled as an elastic surface that is in contact with arigid metal substrate. Due to the weak van der Waals interaction between graphene and metal, thekinematics of the model incorporates sliding of graphene. However, since we assume that grapheneis always in contact with the substrate, its normal displacement is mediated by surface diffusion ofmetal atoms. Based on evidence from recent molecular dynamics simulations and experiments, wemodel the interfacial energy to include in-plane elasticity and bending energy of graphene, and aninteraction energy that depends on the orientation of graphene relative to the substrate. We comparethe predictions of our model with surface reconstructions observed during the CVD of graphene onforged thin film palladium polycrystals. As we continue to unravel the atomic scale mechanismsresponsible for surface reconstruction during CVD, we expect the current continuum frameworkand its generalizations will serve to bridge the atomic- and the meso-scales.
Polycrystal plasticity and grain boundary evolution: A unified dislocation-based diffuse-interface approach [Link]
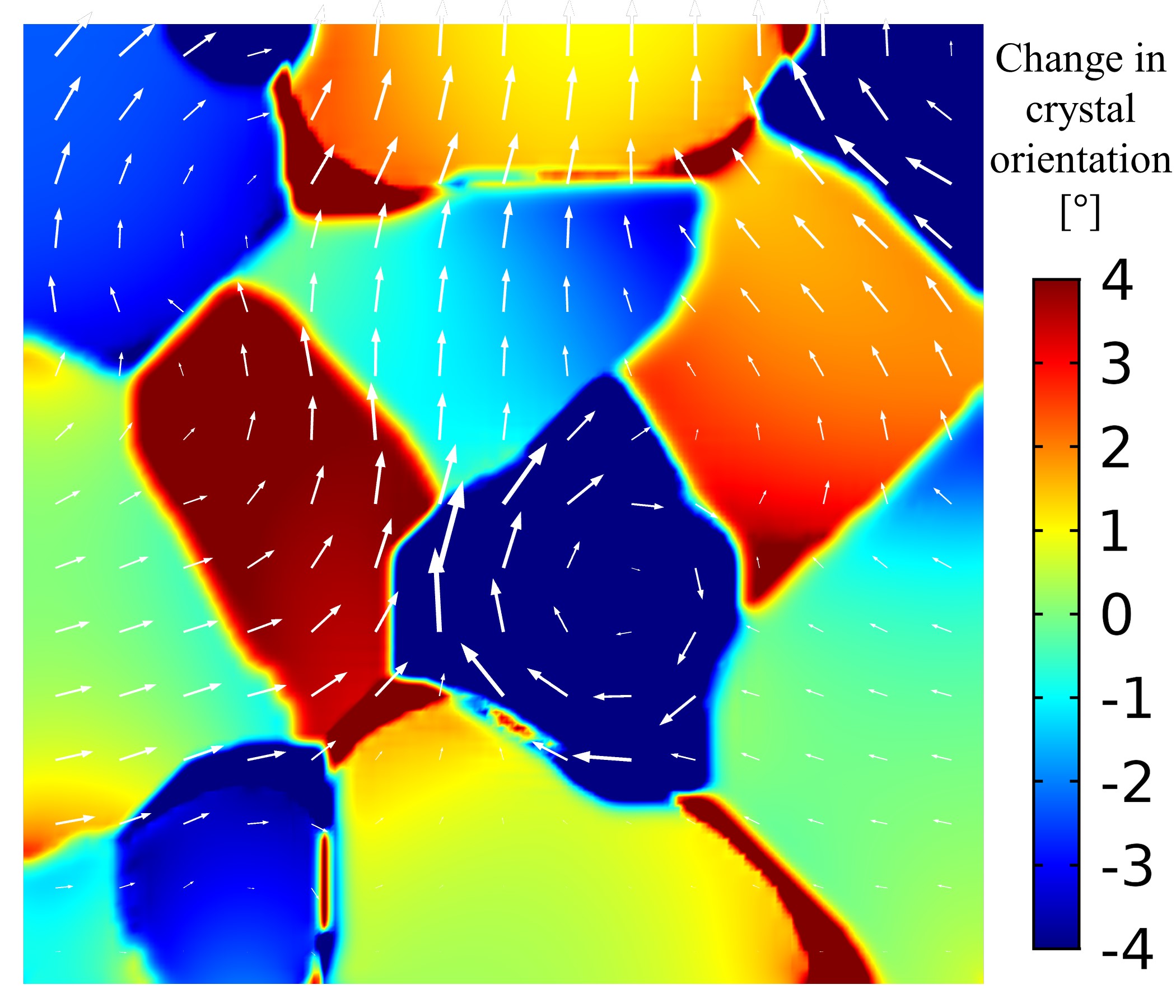 | 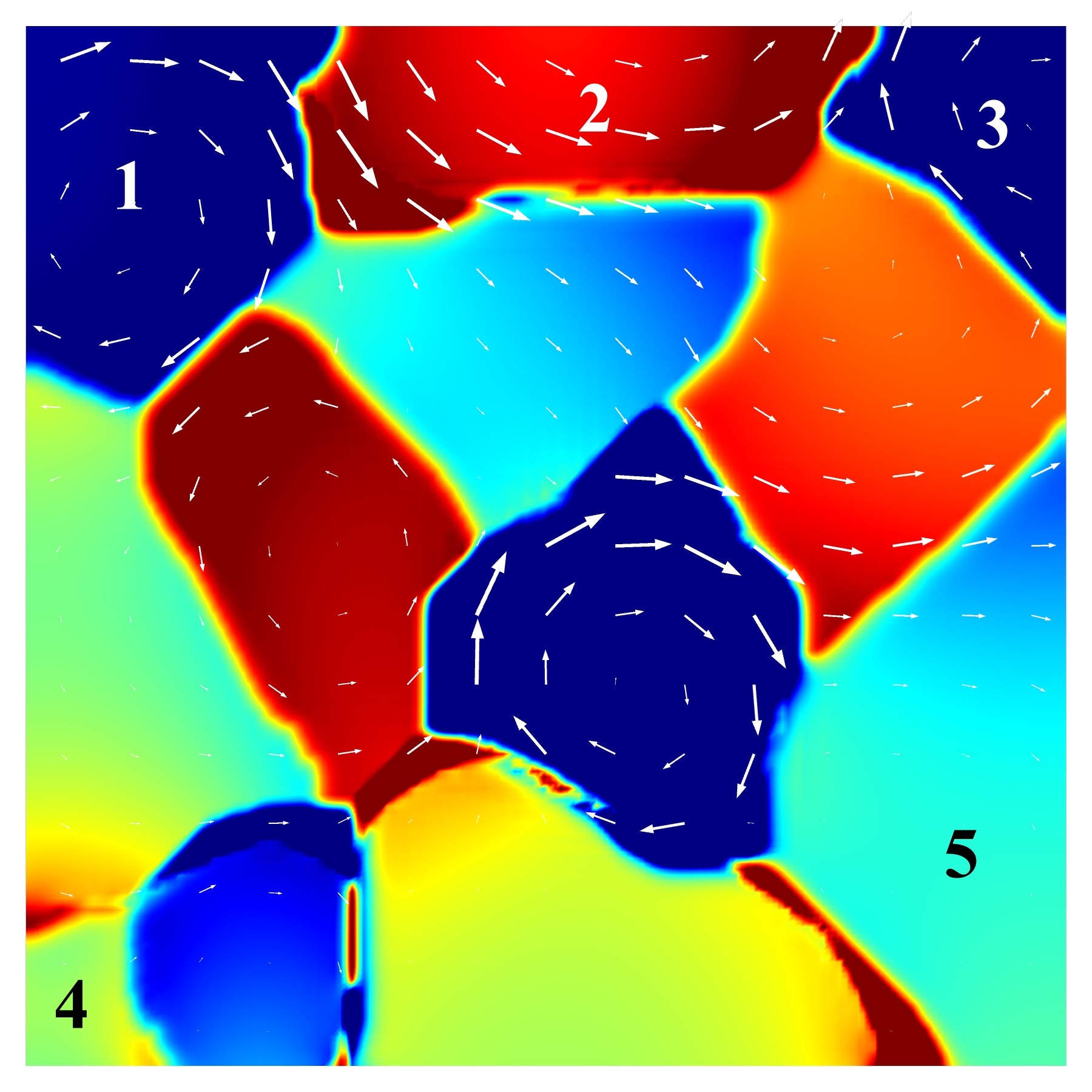 |
Grain structure plays a key role in the mechanical properties of alloy materials. Engineering the grain structure requires a comprehensive understanding of the evolution of grain boundaries (GBs) when a material is subjected to various manufacturing processes. To this end, we present a computationally efficient framework to describe the co-evolution of bulk plasticity and GBs. We represent GBs as diffused geometrically necessary dislocations, whose evolution describes GB plasticity. Under this representation, the evolution of GBs and bulk plasticity is described in unison using the evolution equation for the plastic deformation gradient, an equation central to classical crystal plasticity theories. To reduce the number of degrees of freedom, we present a procedure which combines the governing equations for each slip rates into a set of governing equations for the plastic deformation gradient. Finally, we outline a method to introduce a synthetic potential to drivemigration of a flat GB.
A fast and efficient thresholding algorithm to simulate grain growth in polycrystalline materials [Link]
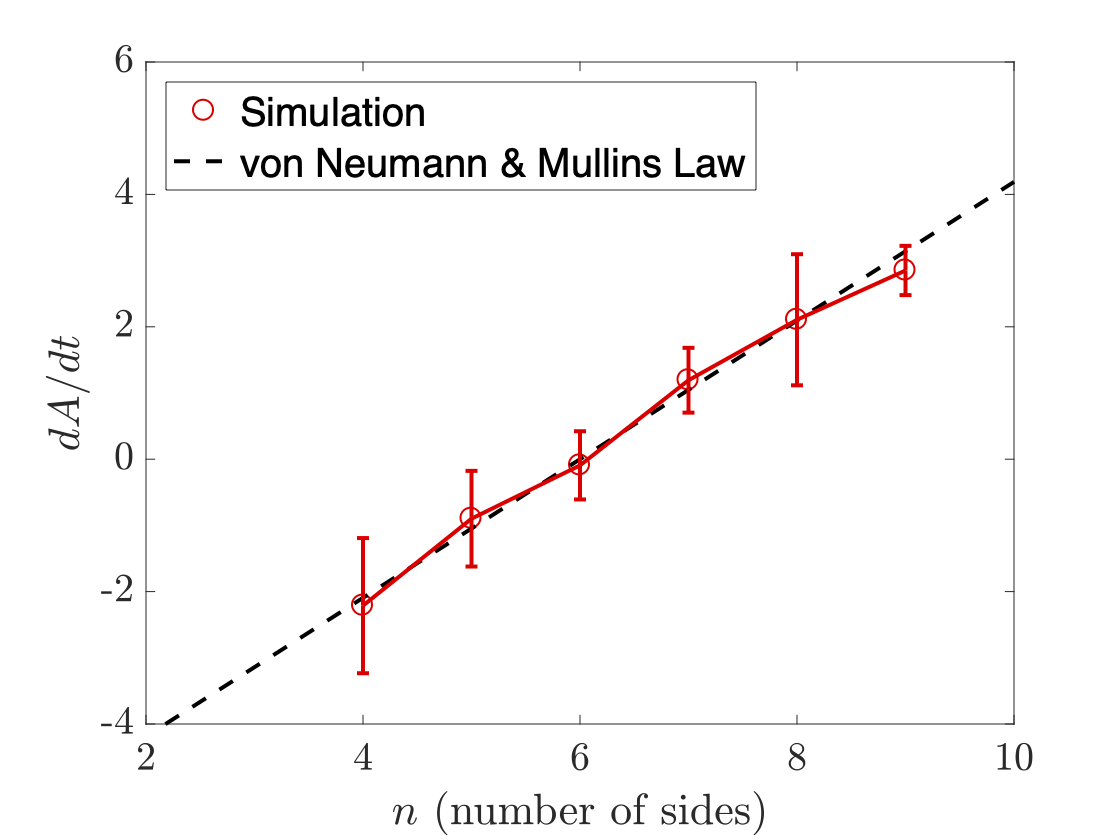 |
One of the most important aims of grain boundary modeling is to predict the evolution of a large collection of grains in phenomena such as abnormal grain growth, coupled grain boundary motion, and recrystallization that occur under extreme thermomechanical loads. A unified framework to study the coevolution of grain boundaries with bulk plasticity has recently been developed by Admal [2018], which is based on modeling grain boundaries as continuum dislocations governed by an energy based on the Kobayashi–Warren–Carter (KWC) model (Kobayashi et al, 1998).
While the resulting unified model demonstrates coupled grain boundary motion and polygonization (seen in recovery), the implementation of the unified model using finite elements inherits the computational challenges of the KWC model that originate from the singular diffusive nature of its governing equations. In this work, we develop a thresholding method that relies on a primal dual algorithm and the fast marching method, resulting in an \(\mathcal O(N \log N)\) algorithm, where \(N\) is the number of grid points. We validate the model by demonstrating the Herring angle and the von Neumann–Mullins relations as shown in the figure on the left.
Recrystallization in refractory materials
 |  |
Microstructural features such as grain size and morphology directly impact the macroscopic properties of a crystalline material. For example, the exceptional strength of a nanostructured alloy is a result of its nano-sized grains which hinder plastic distortion. At elevated temperatures, a material’s microstructure evolves due to the phenomena of recovery, recrystallization and grain growth, thus altering its mechanical properties. One of the most challenging aspects of engineering the microstructure is to ensure its stability in extreme environments. This work originated from the need to improve the efficiency of power plants by developing a quantitative predictive model of recrystallization in refractory materials, in particular tungsten. Increasing the upper operating temperature of a power plant increases its Carnot efficiency. Refractory metals are an important class of materials with extremely high melting points, and thus ideally suited for high temperature industrial applications such as in power plants and nuclear reactors. However, the operating temperature for structural uses is not limited by melting but rather by recrystallization, which typically occurs at temperatures as low as half to one-third of the melting point.
Most models developed in the last two decades to study recovery, recrystallization and grain growth have employed the phase field method, and do not model the entire problem in a unified framework. More importantly, they do not model the underlying plastic deformation/shape change that accompanies grain boundary motion. Therefore, phenomena such as dynamic grain nucleation and shear induced grain boundary motion, which play an important role during recrystallization, are beyond the reach of these models. The aim of this project is to overcome the above stated limitations and model microstructure evolution within a unified framework. In this work, we develop a thermodynamically-consistent model by generalizing the framework of crystal plasticity to polycrystalline materials, and endow the model with grain boundary energy to model grain evolution. We demonstrate that the model can simulate a wide variety of phenomena such as grain nucleation, rotation, shrinking, and shear-induced grain boundary sliding and coupling motions.
Atomistic repsresentation of strain gradient elastic tensors
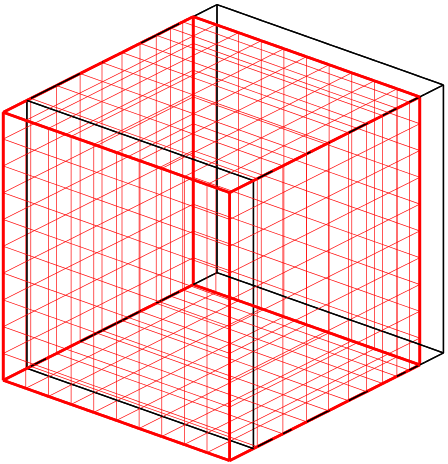 | 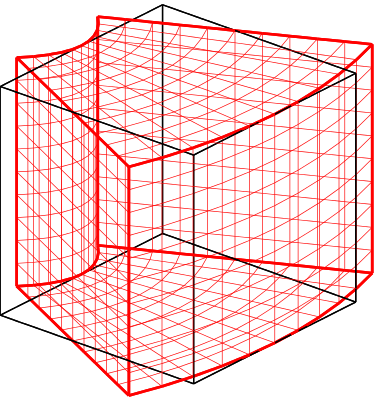 | 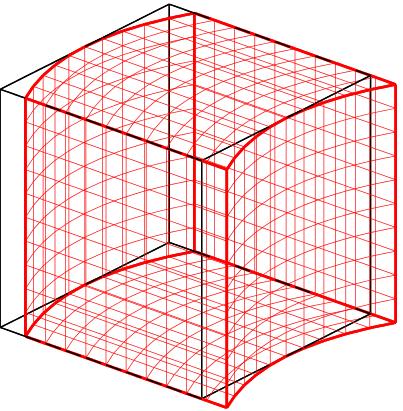 | 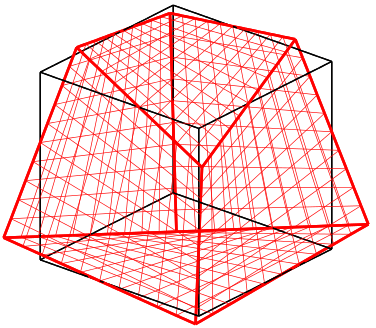 |
In classical elasticity, the strain energy density depends on the first gradient of the deformation map. This assumption leads to an absence of intrinsic length scales in the model, a shortcoming that has a pronounced effect when studying phenomena occurring at multiple scales. For example, surface and strain gradients energies, which are not included in classical elasticity, play an important role in the mechanical behaviour of micro- or nano-sized crystalline systems. Materials commonly referred to as flexoelectric materials exhibit spontaneous polarization in the presence of strain gradients. Flexoelectric materials have the potential to yield a “giant” (500% enhancement relative to conventional piezoelectrics) piezoelectric effect, and therefore have many potential applications such as energy harvesting during locomotion. The above examples highlight the importance of gradient elasticity in technologically important problems.
Stain gradient elasticity (SGE), proposed by Mindlin [1964], is a generalization of classical elasticity to include intrinsic length scales through the dependence of the energy density on strain and its gradient. In other words, SGE includes corrections to the energy corresponding to deformation modes that correspond to strain gradients. The above figure shows such deformation modes in a cubic crystal. Despite its potential, SGE has not gained traction in the engineering community primarily due to the following two issues. First, due to the large number of elastic constants, the theory appears to lack the simplicity of classical elasticity. Second, due to the lack of an explicit relationship between the elastic constants and the underlying atomistic structure, multiscale models that involve gradient elasticity have not been developed.
In this project, we give a rigorous derivation of formulas for gradient elastic constants as explicit functions of potential energy and the geometry of the crystal. This work establishes a direct relationship between the microstructure and the macroscopic elastic constants, thus resulting in a powerful tool to engineer the microstructure.
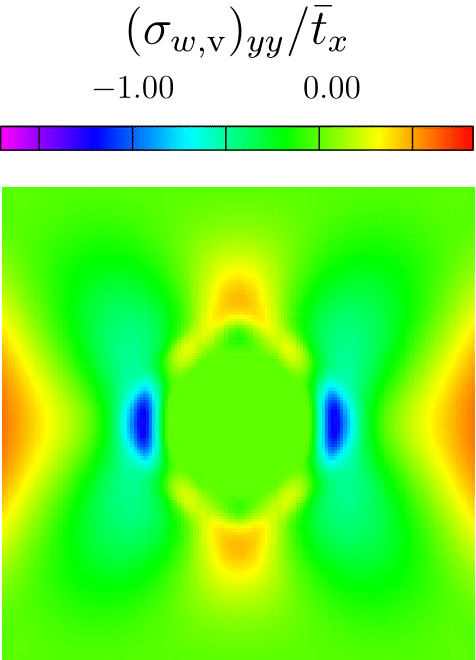
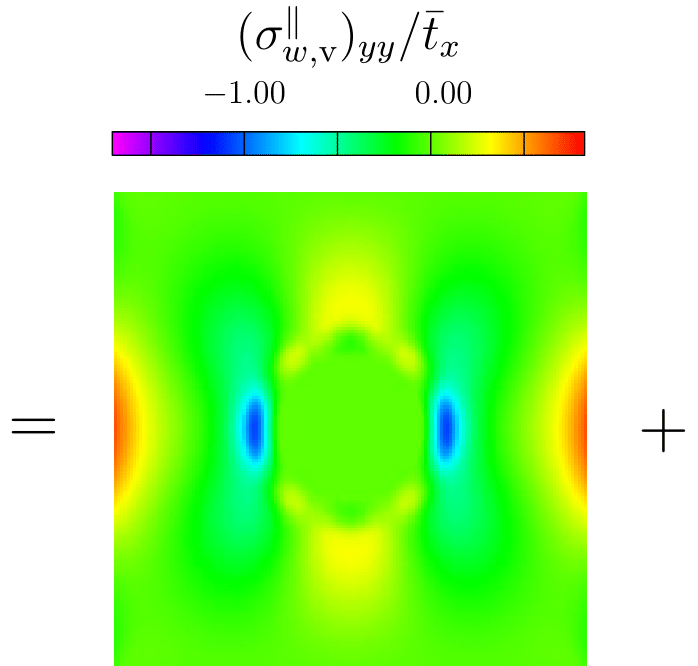
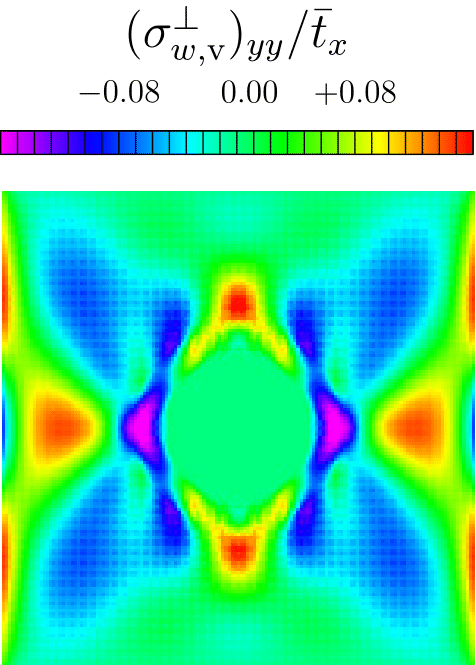
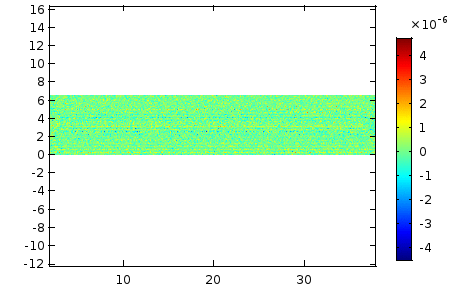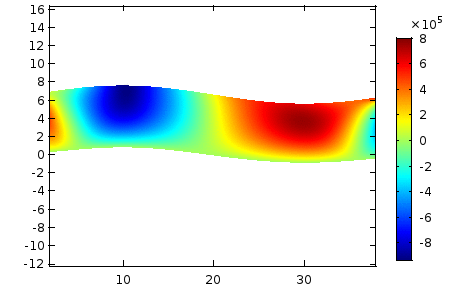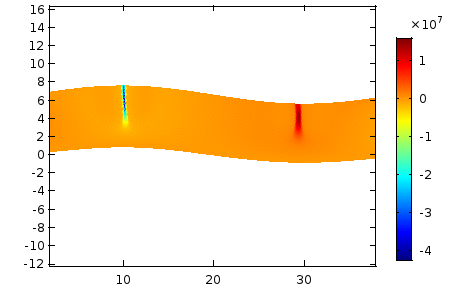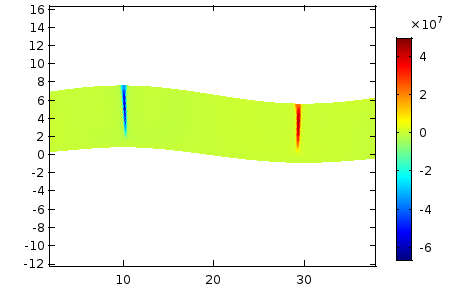
A discrete Helhmholtz Hodge-type decompsition of the atomsitic stress tensor
A central feature of all multiscale methods that involve atomistic and continuum models is the transfer of information between the two models. Information in the continuum model is encoded in the form of continuum fields like energy density, stress, and heat flux, while the information in the atomistic region is in the form of positions and velocities of particles, and atomic forces. In order to transfer information between the two models, definitions for various continuum fields are constructed for the discrete atomistic system. Of all the continuum fields, the stress field for an atomistic system has been a subject of great debate. This is largely due to the existence of numerous and apparently disparate microscopic definitions for stress in the literature. As part of my doctoral thesis, I identified the Irving–Kirkwood (IK) framework as a unified framework and derived existing stress definitions as special cases. In addition, I have proposed new definitions for the energy density and the heat flux vector. These definitions avoid the ambiguous decomposition of energy among particles present in the original IK framework. Additionally, in our study of the non-uniqueness of the atomistic stress tensor, we derived a discrete analog of the Helmholtz decomposition for symmetric stress tensors. The above figure shows the decomposition of the yy-component of the Cauchy stress in a plate with a hole, subjected to uniaxial loading under plane strain conditions. The discrete decomposition of the atomistic stress tensor has potential applications in identifying various defect structures in amorphous materials. On the other hand, the conventional Helmholtz decomposition, which is extensively used in fluid mechanics to identify various features such as vortices and critical points of fluid flow, can also be used for feature detection. Since the discrete decomposition proposed in this work includes the geometry and discreteness of the crystal, it results in a superior resolution of defects compared to the resolution obtained using conventional Helmholtz decomposition.