Quasiconformal deformation of the Sierpinski gasket

The video shows a quasiconformal deformation of the classical Sierpinski gasket SG. In [1] we proved that the infimum of the Hausdorff dimensions of all quasiconformal deformations of SG is equal to one. In fact, one can find a sequence of one-parameter families of planar self-similar iterated function systems whose invariant sets are all quasiconformally equivalent with SG and have Hausdorff dimension decreasing continuously from log 3/log 2 = dim SG towards values arbitrarily close to one.

The following sequence shows “still shots” from one of these one-parameter families.

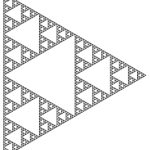
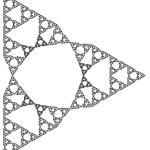
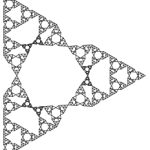
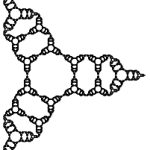
Similar constructions can be made for other self-similar fractals of “gasket type”, e.g., higher-dimensional Sierpinski-type gaskets and polygaskets.

[1] J. T. Tyson and J.-M. Wu, “Quasiconformal dimension of self-similar sets”, Rev. Mat. Iberoamericana 22 (2006), 205-258.

Thanks to Dan Schultz and Nishant Nangia for writing the code which produced the video. Supported by the Illinois Geometry Lab (IGL) in the Department of Mathematics at the University of Illinois at Urbana-Champaign.