Author: Sean Lang
There are 17 equations distributed throughout the Scale, Law and Life piece, each significant in their placement relative to one another. The equations are described below, beginning at the upper-left corner of the drawing and proceeding clockwise around the drawing.
Maxwell’s Equations
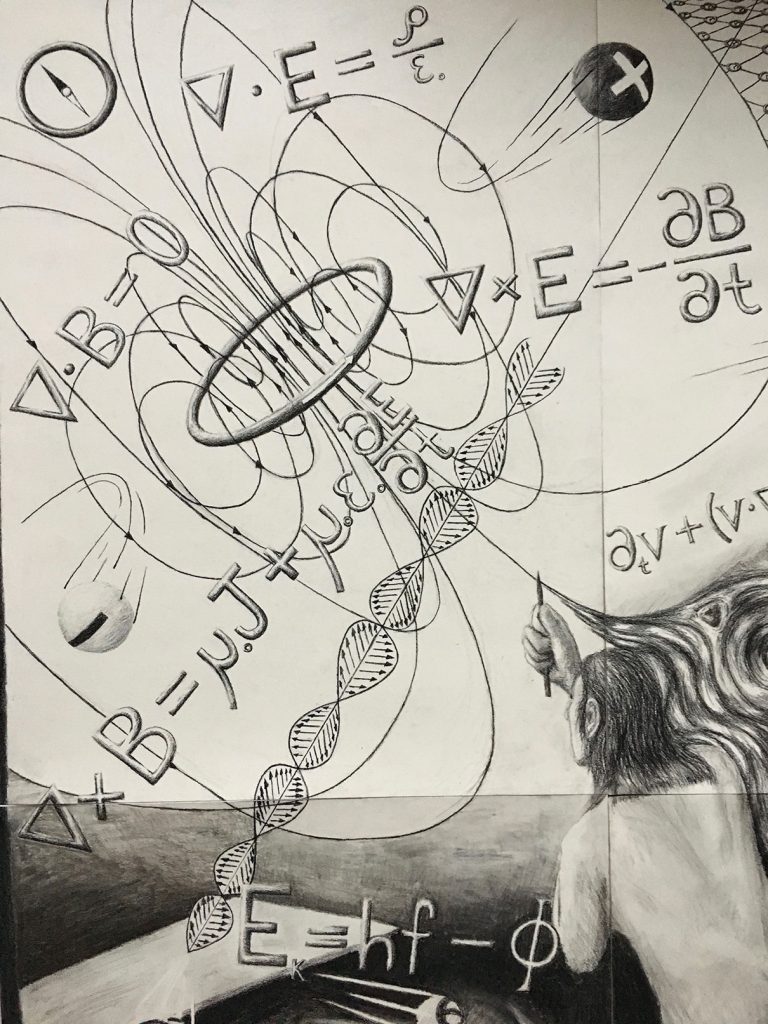 The most important aspect of electromagnetic phenomena to understand is that the presence of electric charges gives rise to electric and magnetic fields which permeate all of space. You’ll notice that two of the four Maxwell Equations are written with an inverted triangle, a dot, and the letters E and B which represent the Electric field and Magnetic field respectively. What this represents is the divergence of the electric and magnetic fields which, put simply, is the ability of these fields to be created radially from a point-source. The divergence of the electric field is dependent on the amount of charge present while the divergence of the magnetic field is zero! This means that, as far as we’re aware, point-sources of the electric field exist while point-sources of the magnetic field do not.
The most important aspect of electromagnetic phenomena to understand is that the presence of electric charges gives rise to electric and magnetic fields which permeate all of space. You’ll notice that two of the four Maxwell Equations are written with an inverted triangle, a dot, and the letters E and B which represent the Electric field and Magnetic field respectively. What this represents is the divergence of the electric and magnetic fields which, put simply, is the ability of these fields to be created radially from a point-source. The divergence of the electric field is dependent on the amount of charge present while the divergence of the magnetic field is zero! This means that, as far as we’re aware, point-sources of the electric field exist while point-sources of the magnetic field do not.
The remaining two Maxwell Equations have a cross symbol instead of a dot. This represents the curl of these fields, rather than their divergence. This can be thought of as a measure of how much the electric and magnetic fields curl or twist in free space. On the right-side of the curl of E equation, one can see a term involving B, and vice-versa. This term in each equation tells us that an Electric field that changes in time will give rise to a Magnetic field, which is curling, and a Magnetic field that changes in time will give rise to an Electric field, which is curling. In the equation describing the curl of B, there is an extra term, involving the letter J, which represents a current of electric charge. It is the case, in fact, that the presence of moving electric charges will give rise to a Magnetic field which is curling! Notice that there is not a ‘magnetic current’ term in the equation describing the curl of E; the reason for this is that ‘magnetic current’ does not exist! If it were the case that magnetic point-sources existed, there would be a ‘magnetic current’ term here, but alas they have not been found to exist.
Together, the equations for the divergence and the curl of the Electric and Magnetic fields (Maxwell’s Equations) offer a complete description of their behavior in the presence of electric charges, stationary or otherwise, as well as in the vacuum of space.
The Navier-Stokes Equation
 This is the lengthy equation located in the upper-middle region of the drawing. A fluid, in its most basic description, is a continuum of massive particles moving at some velocity. This equation can be thought of as Newton’s Second Law (F=ma) as it applies to a viscous, incompressible fluid in motion. It is not a statement of conservation of energy, but rather a representation of a fluid’s response given its viscosity, its collective velocity, and any external pressures.
This is the lengthy equation located in the upper-middle region of the drawing. A fluid, in its most basic description, is a continuum of massive particles moving at some velocity. This equation can be thought of as Newton’s Second Law (F=ma) as it applies to a viscous, incompressible fluid in motion. It is not a statement of conservation of energy, but rather a representation of a fluid’s response given its viscosity, its collective velocity, and any external pressures.
The Continuity Equation
 This equation is just below the Navier-Stokes equation, between the top two humans. An essential characteristic of a system in fluid mechanics is the presence or lack thereof any fluid sources or sinks. If we imagine an enclosed region within a fluid, we can ask the question: How much fluid is leaving this region and how much is entering? In, say, a bucket of water with no holes, we’d certainly expect that the amount of water leaving an enclosed region is precisely the same as the amount entering that region! After all, the fluid is continuous! If this is the case, the Greek letter sigma, representing the presence of a fluid source or sink, is equal to zero! The other terms in the equation, from left to right, represent the amount of fluid mass entering or leaving the enclosed region per unit time and the divergence of the fluid current.
This equation is just below the Navier-Stokes equation, between the top two humans. An essential characteristic of a system in fluid mechanics is the presence or lack thereof any fluid sources or sinks. If we imagine an enclosed region within a fluid, we can ask the question: How much fluid is leaving this region and how much is entering? In, say, a bucket of water with no holes, we’d certainly expect that the amount of water leaving an enclosed region is precisely the same as the amount entering that region! After all, the fluid is continuous! If this is the case, the Greek letter sigma, representing the presence of a fluid source or sink, is equal to zero! The other terms in the equation, from left to right, represent the amount of fluid mass entering or leaving the enclosed region per unit time and the divergence of the fluid current.
The Lorentz Transformation
This equation is located above the Navier-Stokes equation, among the gird-like structure at the top-center of the drawing. Before Albert Einstein developed his Theory of Special relativity, relative motion was understood by implementing the Galilean Transformation. With this picture, the phenomena of time-dilation and length-contraction of object in motion were not factored into their 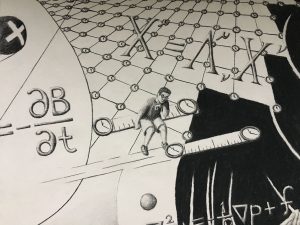 temporal and spatial description. Once Einstein had determined that the speed of light is constant in all frames of reference, he formulated a transformation of a different nature, later known as the Lorentz Transformation. This transformation accounts for the fact that objects in motion, as measured by a stationary observer, proceed through time and space at a different rate depending on their relative velocity. As the Lorentz Transformation is represented in the drawing, the big X’s represent the assigned space and time coordinates for the observer and the observed. The Greek symbol Lambda, a 4×4 matrix, is the object doing the transforming and contains information about the object’s velocity relative to the observer.
temporal and spatial description. Once Einstein had determined that the speed of light is constant in all frames of reference, he formulated a transformation of a different nature, later known as the Lorentz Transformation. This transformation accounts for the fact that objects in motion, as measured by a stationary observer, proceed through time and space at a different rate depending on their relative velocity. As the Lorentz Transformation is represented in the drawing, the big X’s represent the assigned space and time coordinates for the observer and the observed. The Greek symbol Lambda, a 4×4 matrix, is the object doing the transforming and contains information about the object’s velocity relative to the observer.
Einstein’s Generalized Field Equation
This is the lengthy equation below the black hole in the upper-right frame. In Einstein’s Theory of General Relativity, this equation is the grand, field equation which describes how the fabric of space time curves and twists given the  presence of matter and energy. The solution one finds from this equation is the space-time metric, represented by the lower-case g’s, which can be thought of as a kind of characteristic signature of the space-time fabric in a certain system. By knowing this space-time metric, we can determine what the behavior of an object will be in this system because, simply put, the curvature of space-time directs the objects present. This ‘directing’ of objects, based on the curvature of the surrounding space-time fabric, is what we perceive as the force of gravity.
presence of matter and energy. The solution one finds from this equation is the space-time metric, represented by the lower-case g’s, which can be thought of as a kind of characteristic signature of the space-time fabric in a certain system. By knowing this space-time metric, we can determine what the behavior of an object will be in this system because, simply put, the curvature of space-time directs the objects present. This ‘directing’ of objects, based on the curvature of the surrounding space-time fabric, is what we perceive as the force of gravity.
Bekenstein-Hawking Entropy from Black Holes
This equation is located in the upper-right corner of the drawing. As a young man studying black holes, Stephen Hawking conceived of a mechanism by which a black hole can eject its own mass and, eventually, evaporate altogether. The idea is based on the nature of the vacuum as viewed through the lens of quantum mechanics. According to our understanding of quantum mechanics, the vacuum  is filled with particle-antiparticle pairs coming in and out of existence by creation and annihilation with one another. Hawking theorized that if such an event were to occur near the Schwarzschild radius of a black hole, the point at which light can no longer escape, one of these particles could fall in and one could escape. By this mechanism, it is as if the black hole is emitting its own matter and this is what physicists call Hawking radiation. Bekenstein-Hawking Entropy describes the entropy necessarily present at the surface of a black hole in order to comply with the thermodynamic principles governing the matter exterior to the black hole’s event horizon.
is filled with particle-antiparticle pairs coming in and out of existence by creation and annihilation with one another. Hawking theorized that if such an event were to occur near the Schwarzschild radius of a black hole, the point at which light can no longer escape, one of these particles could fall in and one could escape. By this mechanism, it is as if the black hole is emitting its own matter and this is what physicists call Hawking radiation. Bekenstein-Hawking Entropy describes the entropy necessarily present at the surface of a black hole in order to comply with the thermodynamic principles governing the matter exterior to the black hole’s event horizon.
Einstein’s Mass-Energy Relation
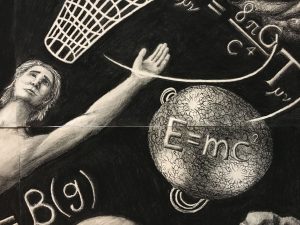 This equation is located within the star, just below Einstein’s Generalized Field Equation, and is perhaps the most famous equation in all of physics. While many know by name, its meaning can be somewhat elusive and is only understood through the formulation of relativistic mechanics. The reason this relation is so powerful is that it is an explicit statement that Energy is Mass, and vice-versa, for matter which isn’t moving through space at some rate. There is, in fact, a more general Mass-Energy relation, being: . Photons, particles which have no mass carry the relation when goes to zero. Then we get back the relation, the Energy of a Mass which has no Momentum.
This equation is located within the star, just below Einstein’s Generalized Field Equation, and is perhaps the most famous equation in all of physics. While many know by name, its meaning can be somewhat elusive and is only understood through the formulation of relativistic mechanics. The reason this relation is so powerful is that it is an explicit statement that Energy is Mass, and vice-versa, for matter which isn’t moving through space at some rate. There is, in fact, a more general Mass-Energy relation, being: . Photons, particles which have no mass carry the relation when goes to zero. Then we get back the relation, the Energy of a Mass which has no Momentum.
Renormalization Group Equation
This equation is split diagonally across the Earth, in the center of the drawing. The Renormalization Group Equation is utilized to determine how a physical system behaves at different scales. In the analogous sense that a microscope might be the appropriate tool for studying bacteria but not macroscopic objects,  this equation is a means by which a physicist can determine what mathematical tools would be appropriate to apply to a physical system at some physical or energetic scale. This equation is useful in studying the necessary changes in the parameters of a theory as the scale under consideration is changed. Additionally, the use of such an expression can indicate which theories are valid at all energy scales – conformal field theories – and these theories are of great importance in a variety of areas in physics including Condensed Matter Physics, String Theory, and Gauge-Gravity Dualities (Holography).
this equation is a means by which a physicist can determine what mathematical tools would be appropriate to apply to a physical system at some physical or energetic scale. This equation is useful in studying the necessary changes in the parameters of a theory as the scale under consideration is changed. Additionally, the use of such an expression can indicate which theories are valid at all energy scales – conformal field theories – and these theories are of great importance in a variety of areas in physics including Condensed Matter Physics, String Theory, and Gauge-Gravity Dualities (Holography).
Newton’s Second Law
This equation is located to the right of the space shuttle. At the macroscopic scale, when objects are moving at speeds which are slow compared to the speed of light, the force exerted on an object is equivalent to its mass multiplied by its  acceleration. This equation is at the base of humans’ understanding of forces, and it applies to countless areas of study. Represented below is the equation which is simply another more general way of expressing the force on an object. The meaning of is, simply put, the change in an object’s momentum per unit time. The reason this expression is more general is that it accounts not only for the possibility of a change in the velocity of some mass, but also of the object’s mass changing as well. After all momentum is dependent on both mass and velocity and so, if either of these quantities change in time, a force is being exerted.
acceleration. This equation is at the base of humans’ understanding of forces, and it applies to countless areas of study. Represented below is the equation which is simply another more general way of expressing the force on an object. The meaning of is, simply put, the change in an object’s momentum per unit time. The reason this expression is more general is that it accounts not only for the possibility of a change in the velocity of some mass, but also of the object’s mass changing as well. After all momentum is dependent on both mass and velocity and so, if either of these quantities change in time, a force is being exerted.
The artist has depicted the expressions and recoiling away from one another to capture the idea of Newton’s Third Law, which states that, for every force exerted, there will be another force equal and opposite to it in the absence of external influences.
The Third Law of Thermodynamics
This equation is located just below the strand of DNA.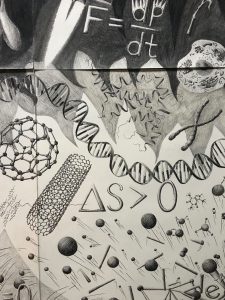 The Third Law of Thermodynamics states that, in an isolated system, the entropy of that system can only increase. Said simply, entropy is a measure of the amount of ways in which a system can be configured. Consider, for instance, a bunch of atoms in an enclosed box, isolated from any kind of energy exchange. If we consider a comparison between the number of ways in which these atoms could be grouped into the box’s corner and the number of ways in which the atoms could be dispersed among the box’s total volume, we can conclude that there are an unimaginably greater number of ways for the latter configuration to exist. This is the central idea behind entropy. An isolated system will always have the tendency to configure itself in the state which, for lack of a better term, is ‘most possible.’
The Third Law of Thermodynamics states that, in an isolated system, the entropy of that system can only increase. Said simply, entropy is a measure of the amount of ways in which a system can be configured. Consider, for instance, a bunch of atoms in an enclosed box, isolated from any kind of energy exchange. If we consider a comparison between the number of ways in which these atoms could be grouped into the box’s corner and the number of ways in which the atoms could be dispersed among the box’s total volume, we can conclude that there are an unimaginably greater number of ways for the latter configuration to exist. This is the central idea behind entropy. An isolated system will always have the tendency to configure itself in the state which, for lack of a better term, is ‘most possible.’
The Partition Function
This equation is in the lower-right corner of the drawing. When determining the  probability of a system to take on a certain configuration, especially its configuration in equilibrium, the partition function is the most useful tool in our toolbox. The partition function depends on the number of degrees of freedom a system has, as well as if the physical states characterizing the system are said to be continuous or discrete. The most important quantities of a system, from a Statistical Mechanics standpoint: Free Energy, Entropy, Pressure, etc., can be represented in some way by the partition function and its derivatives.
probability of a system to take on a certain configuration, especially its configuration in equilibrium, the partition function is the most useful tool in our toolbox. The partition function depends on the number of degrees of freedom a system has, as well as if the physical states characterizing the system are said to be continuous or discrete. The most important quantities of a system, from a Statistical Mechanics standpoint: Free Energy, Entropy, Pressure, etc., can be represented in some way by the partition function and its derivatives.
The Quantum Harmonic Oscillator
This equation is just below the Earth, in the center of the drawing. The simplest harmonic oscillator that exists is a simple pendulum, its arm oscillating uniformly in gravity. A quantum harmonic oscillator is fundamentally different from a macroscopic pendulum in that the thing that’s oscillating is a particle, such as an electron, and its oscillations are limited to a set of discrete values. This idea is fundamental to the nature of Quantum Mechanics and matter particles at the quantum scale. The artist has represented the shape of the quantum harmonic oscillator as a parabola because the definition of this object is essentially a potential barrier, confining the oscillating particles.
 As represented in the drawing, if an electron occupying some energy state in a quantum harmonic oscillator drops down to a lower energy state, a photon yielding precisely the energy difference will be emitted from the oscillator. The wavelength of the emitted photon is representative of its energy in that a photon with a long wavelength has less energy than a photon with a short wavelength. The reverse of this process can also take place; a photon can interact with an electron in a quantum harmonic oscillator and excite it to a higher energy state, again corresponding to the energy which was carried by the photon.
As represented in the drawing, if an electron occupying some energy state in a quantum harmonic oscillator drops down to a lower energy state, a photon yielding precisely the energy difference will be emitted from the oscillator. The wavelength of the emitted photon is representative of its energy in that a photon with a long wavelength has less energy than a photon with a short wavelength. The reverse of this process can also take place; a photon can interact with an electron in a quantum harmonic oscillator and excite it to a higher energy state, again corresponding to the energy which was carried by the photon.
The Principle of Least Action
This equation is at the bottom-center of the drawing. This principle underlies our deepest understanding of physics across nearly all its sub-fields. The Principle of Least Action essentially states that we can determine the behavior of a physical system by asking the question: Is there some quantity which nature is minimizing  or, more generally, making stationary. An excellent example of this idea can be given by considering the behavior of light as it passes from one medium to another (from air to water, for instance). What path does the light take? Well, it so happens that light, when traversing the distance between some point A and another point B, minimizes the amount of time it takes to travel that distance! By understanding this principle, we know that light’s path of travel should bend as it transitions from one medium to another. This is far from the only example of a minimization principle in nature. In fact, minimization principles are used prevalently in the studies of Classical Mechanics, Electromagnetism, General Relativity, Quantum Mechanics, and in many more. At all scales, nature seems to tell us that the simplest way to determine the behavior of a complex physical system is by using such a minimization principle.
or, more generally, making stationary. An excellent example of this idea can be given by considering the behavior of light as it passes from one medium to another (from air to water, for instance). What path does the light take? Well, it so happens that light, when traversing the distance between some point A and another point B, minimizes the amount of time it takes to travel that distance! By understanding this principle, we know that light’s path of travel should bend as it transitions from one medium to another. This is far from the only example of a minimization principle in nature. In fact, minimization principles are used prevalently in the studies of Classical Mechanics, Electromagnetism, General Relativity, Quantum Mechanics, and in many more. At all scales, nature seems to tell us that the simplest way to determine the behavior of a complex physical system is by using such a minimization principle.
The Schrödinger Equation
 This equation resides among the waves in the lower-left panel. The Schrödinger Equation is the mathematical gem of Quantum Mechanics, describing the wave-like behavior of particles in the presence of potential energy or in free-space. The artist has represented the equation in its most concise form, with the so-called Hamiltonian operator acting upon the wave-function, the Greek letter Psi, equaling the Energy of the system multiplied again by Psi. The wave-function is a mathematical expression carrying probabilistic information about the energy state of the system, such that when acted upon by the Hamiltonian operator, the system’s energy is outputted explicitly.
This equation resides among the waves in the lower-left panel. The Schrödinger Equation is the mathematical gem of Quantum Mechanics, describing the wave-like behavior of particles in the presence of potential energy or in free-space. The artist has represented the equation in its most concise form, with the so-called Hamiltonian operator acting upon the wave-function, the Greek letter Psi, equaling the Energy of the system multiplied again by Psi. The wave-function is a mathematical expression carrying probabilistic information about the energy state of the system, such that when acted upon by the Hamiltonian operator, the system’s energy is outputted explicitly.
Heisenberg’s Uncertainty Principle
This principle is in the lower-left corner of the drawing. The Uncertainty Principle is a statement that says, due to the wave-nature of particles at the quantum scale, the position and momentum of a particle can never be measured simultaneously,  with equal certainty. Imagine in your mind a wave traveling through space. Ask yourself: Where is that wave, exactly? The wave you’ve imagined is likely one of constant wavelength, is it not? Waves of constant wavelength have a precise momentum, and so it would be impossible to say that this wave is located precisely here, or precisely there. Now, if you imagined a wave-packet, that is a more localized wave consisting of various wavelengths, then you’ve imagined a situation in which the wave can be located in space with a higher certainty. However, by adding several wavelengths, you’ve increased the uncertainty in the momentum of this wave-packet. This is the nature of the Uncertainty Principle. The artist has depicted this idea by writing the uncertainty relation of position and momentum inside a graphical plot of the statistical quantities associated with position and momentum; namely, their standard deviations.
with equal certainty. Imagine in your mind a wave traveling through space. Ask yourself: Where is that wave, exactly? The wave you’ve imagined is likely one of constant wavelength, is it not? Waves of constant wavelength have a precise momentum, and so it would be impossible to say that this wave is located precisely here, or precisely there. Now, if you imagined a wave-packet, that is a more localized wave consisting of various wavelengths, then you’ve imagined a situation in which the wave can be located in space with a higher certainty. However, by adding several wavelengths, you’ve increased the uncertainty in the momentum of this wave-packet. This is the nature of the Uncertainty Principle. The artist has depicted this idea by writing the uncertainty relation of position and momentum inside a graphical plot of the statistical quantities associated with position and momentum; namely, their standard deviations.
The Dirac Equation
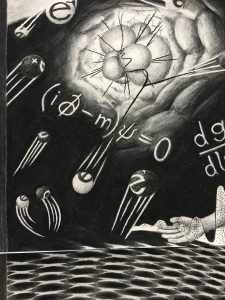 This equation is below the blast in the left-most panel. The Dirac Equation can be said to be the relativistic counterpart of the Schrödinger equation. This equation is consistent with both Quantum Mechanics and Special Relativity, and it encodes details necessary to explaining the spin-nature of matter particles.
This equation is below the blast in the left-most panel. The Dirac Equation can be said to be the relativistic counterpart of the Schrödinger equation. This equation is consistent with both Quantum Mechanics and Special Relativity, and it encodes details necessary to explaining the spin-nature of matter particles.
The Photoelectric Effect
This equation is above the blast in the left-most panel. The Photoelectric Effect is the lesser known discovery of Einstein’s, the discovery for which he received his only Nobel Prize. The idea behind this effect is that, when particles of light are 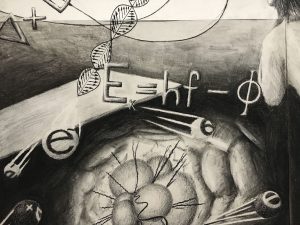 shone onto a metal surface, electrons are emitted from the surface with some amount of Kinetic energy. However, the astounding insight of the Photoelectric Effect is that the Kinetic energy of the emitted electrons is not dependent on the intensity of the light, but rather its frequency! This was one of the important clues leading physicists to the idea of discretized energy states as described by Quantum Mechanics. In the drawing, the Photoelectric effect is written such that the Kinetic energy of the electrons is equal to Planck’s constant multiplied by the frequency of the light, minus the Greek letter Phi, representing the so-called Work Function. This function is essentially the work need to remove the electrons from their bound energy state within the metal, regardless of the incoming light’s energy.
shone onto a metal surface, electrons are emitted from the surface with some amount of Kinetic energy. However, the astounding insight of the Photoelectric Effect is that the Kinetic energy of the emitted electrons is not dependent on the intensity of the light, but rather its frequency! This was one of the important clues leading physicists to the idea of discretized energy states as described by Quantum Mechanics. In the drawing, the Photoelectric effect is written such that the Kinetic energy of the electrons is equal to Planck’s constant multiplied by the frequency of the light, minus the Greek letter Phi, representing the so-called Work Function. This function is essentially the work need to remove the electrons from their bound energy state within the metal, regardless of the incoming light’s energy.