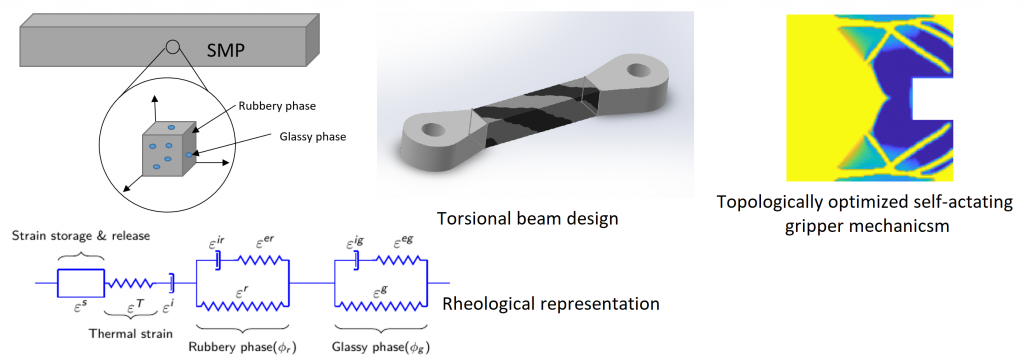
Research
Topology Optimization of Self-Actuating Mechanisms Containing Active Materials
By systematically combining active and passive materials within a single structure or mechanism, one can tailor the strain response of the system to achieve a target motion. Topology optimization provides a means with which to mathematically determine the optimal distribution and layout of the constituent materials in order to obtain the desired displacement response. This design process contains many mathematical and scientific challenges that we seek to address through this research. At the CDI Lab, we are working to develop novel computational techniques for modeling active materials such as shape memory polymers and shape memory alloys, which we then incorporate into our design optimization algorithms to automatically generate optimal material layouts for self-actuating mechanisms. The optimized designs are then fabricated via 3D printing, and validated in the lab. The figure on the right shows a multi-material self-tying knot, whose motion is encoded into its material layout.
Design of a Bi-Stable Morphing Airfoil Via Topology Optimization
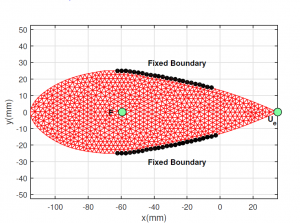
Finite element mesh and boundary conditions
The objective of the project is to harness the geometric nonlinearity of structures to design a novel camber morphing mechanism for a bi-stable airfoil using topology optimization. Morphing can be defined as an external shape change of a structure which has the potential to dramatically alter its performance. Wing morphing can broadly be summarized as continuous shape change of the wing between different configurations whereby the whole structure moves as a single entity, thus eliminating the gaps between hinged members (flaps and slats) in conventional aircraft. Structural morphing confers significant performance benefits including reduced noise, vibrations, and parasitic drag.
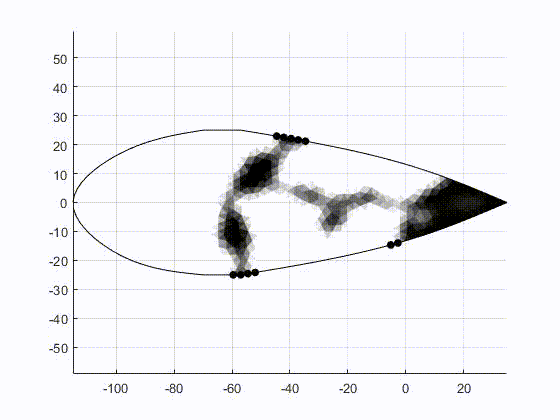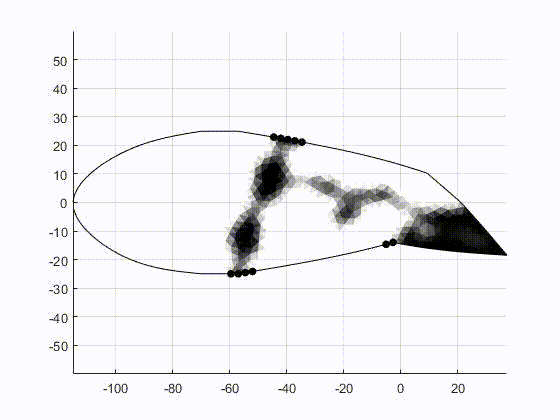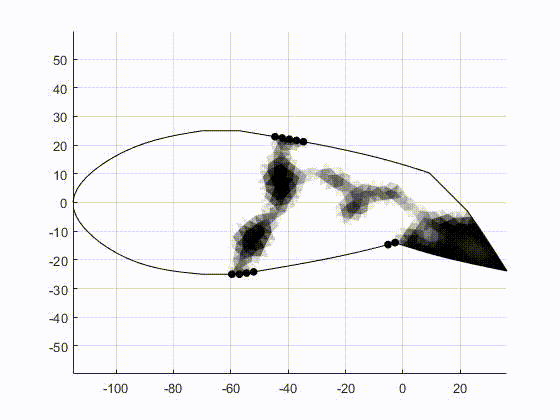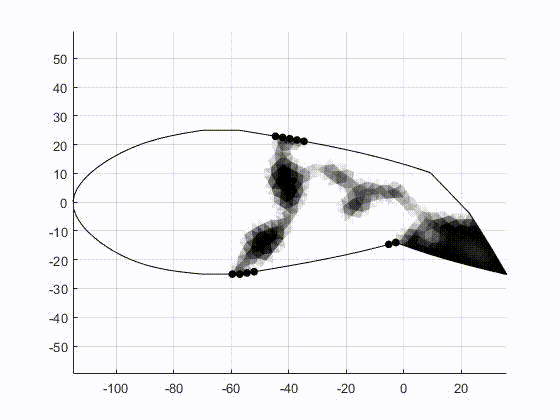 The figure above shows the finite element mesh and boundary conditions for the optimization problem. By optimally distribution material within this region, we can tailor the non-linear force-displacement response to achieve a bi-stable structure. Once the structure is made bi-stable, it can be deployed to dynamically adapt to changing flight conditions, enabling optimal performance in multiple flight regimes.
The figure above shows the finite element mesh and boundary conditions for the optimization problem. By optimally distribution material within this region, we can tailor the non-linear force-displacement response to achieve a bi-stable structure. Once the structure is made bi-stable, it can be deployed to dynamically adapt to changing flight conditions, enabling optimal performance in multiple flight regimes.
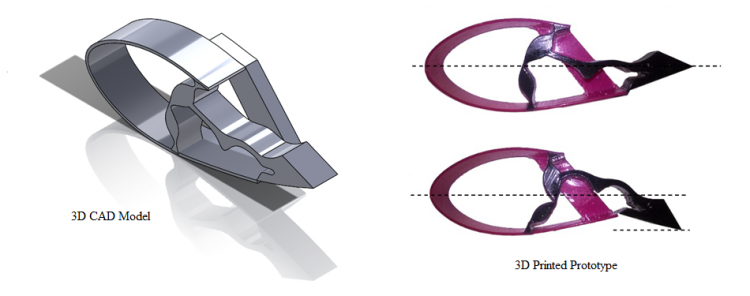
3D Airfoil prototype
Optimal Design of a Hyper-Elliptic Cambered Span (HECS) Wing
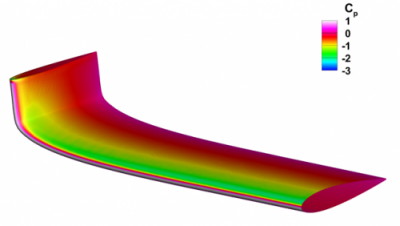
Optimized hyperelliptic cambered wing
Span-optimized configurations are achieved using a Langrange multiplier method coupled with a vortex lattice analysis code. This study explored a diverse range of planform configurations such as rectangular, tapered and elliptic.
Analysis of a rectangular planform cambered span configuration reveals a net reduction of 16.75 % in drag at a design CL of 0.43. Comparisons were made with a baseline planar configuration with Elliptic span loading. Both designs had an equal projected span with the HECS configuration having a larger wetted surface area.
Multi-Material/Multi-Physics Design
The objective of this research is to create an original computational design framework for the optimal design of multifunctional, heterogeneous material systems. New advances in additive manufacturing have made possible the rapid and inexpensive fabrication of complex designs containing multiple classes of materials, including metals, ceramics, and polymers, all within a single print job. This capability allows manufacturers to produce heterogeneous, multi-component designs, without the need for assembly, thereby eliminating the cost and design limitations that assembly entails. In addition to parameterizing the design problem to allow for multiple materials, we must implement coupled, multi-physics finite element analysis models that can simulate multiple material response phenomena (i.e. plasticity, brittle damage, hyperelasticity), within a single system. Within this research thrust, we are exploring several application domains, including
- Thermomechanical design
- Adaptive morphing using shape-memory alloys
- Design for additive manufacturing
Figure below shows an example of multi-material topology optimization for maximum elastic stiffness subject to temperature constraints. The structure must function as a bridge, withstanding a three-point bending load, and it must also function as a heat sink. In response to an applied thermal load at the bottom surface, the design must effectively dissipate heat energy the prevent excess heating along the top surface. The thermal response is modeled using a linear steady-state thermal conductivity model.
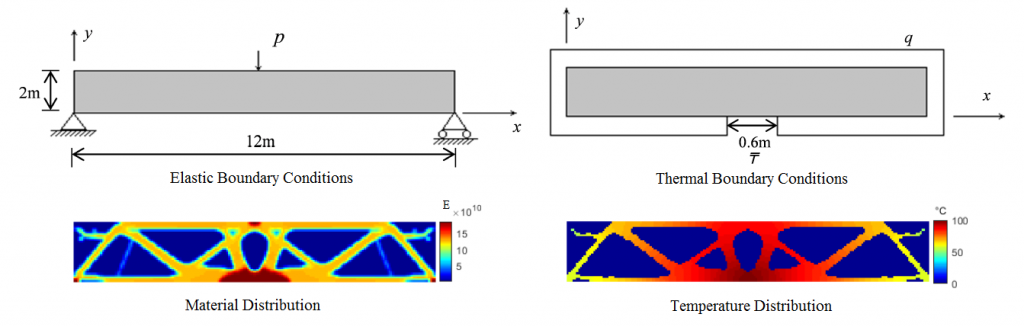
Thermoelastic optimization