Gain function approximation in the feedback particle filter
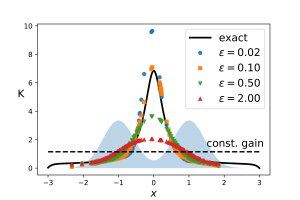
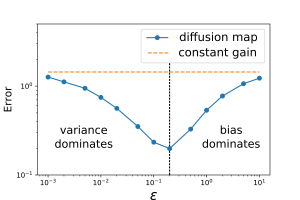
The main challenges in implementing the FPF algorithm is the gain function approximation problem. The gain function is the solution of a Poisson equation involving a probability-weighted Laplacian. The numerical problem is to approximate this solution using only particles sampled from the probability distribution. In order to solve this problem, I introduced a numerical algorithm based on the diffusion-map approximation. The basic idea is to formulate a fixed-point problem using the semigroup associated with the weighted Laplacain. Then, I used the diffusion-map approximation of the semigroup to express the fixed-point problem in terms of particles and use the method of successive approximation to solve it. I also carried out the error analysis of the approximation and I derived error estimates for bias and variance error.
- A. Taghvaei, P. G. Mehta. S. P. Meyn, Error Estimates for the Kernel Gain Function Approximation in the Feedback Particle Filter, IEEE American Control Conference (ACC), Seattle, May 2017. (arXiv)
- A. Taghvaei, P. G. Mehta, Gain Function Approximation in the Feedback Particle Filter, IEEE Conference on Decision and Control (CDC), Las Vegas, December 2016. (arXiv)
Error analysis of the linear feedback particle filter
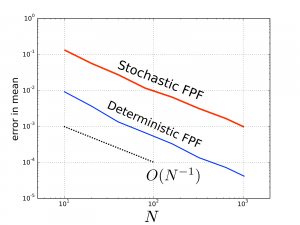
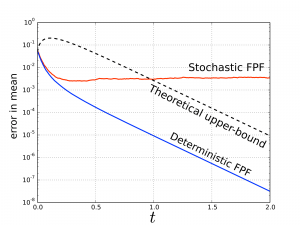
The objective is to study the accuracy, and long-term stability analysis of the FPF algorithm in linear-Gaussian setting. In the mean-field limit, it is known that the empirical distributions of the particles is equal to the posterior distribution. However, little is known when the number of particles is finite. I used Lyapunov stability method to show that the mean-field limit is well-defined and stable; and I proved mean-square error bounds for the accuracy of the filter. I showed that the error stays uniform in time and convergence to zero as the number of particles increase. I performed the analysis for both stochastic and deterministic versions of the FPF algorithm and illustrated their difference.
- A. Taghvaei, P. G. Mehta, Error analysis of the stochastic linear feedback particle filter, IEEE Conference on Decision and Control (CDC), Miami Beach, December 2018. (arXiv)
- A. Taghvaei, P. G. Mehta, Error analysis of the linear feedback article filter, In Proc. of the 2018 American control conference (ACC), Milwaukee, June, 2018 (arXiv)
Optimal transport feedback particle filter

The objective is to design a unique control law for the system of particles in FPF
so that the empirical distribution of the particles approximates the posterior distribution.
In order to so, I used the idea of modeling the filtering task as an optimal transportation
problem from the prior distribution to the posterior distribution. Then, I used a time stepping procedure from sequence of optimal transport maps to construct a unique control law. This procedure led to the formulation of the optimal transport FPF which differs from the original FPF by replacing stochastic terms with deterministic terms
- A. Taghvaei, P. G. Mehta. An Optimal Transport Formulation of Linear Feedback Particle Filter, In Proc. of the 2016 American Control Conference (ACC), Boston, June 2016.(arXiv)
Optimization landscape in linear neural networks
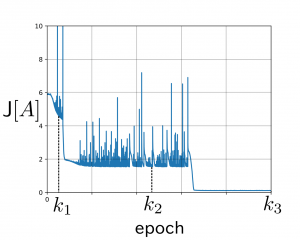
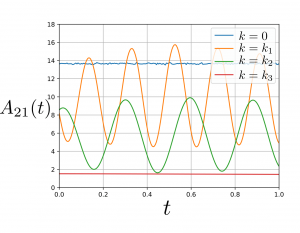
The objective of this project is to gain theoretical insight about the optimization problem in deep learning. For that purpose, I considered the problem of representing and learning a linear transformation using a linear neural network. The main question I answered in this project is related to the existence and optimality properties of the critical points of the optimization problem with mean-squared loss function. Additionally, I studied the robustness of these critical points in the face of (a small amount of) regularization. The methodology is based on the control theory.
- A. Taghvaei, J. W. Kim, P. G. Mehta, How regularization affects the critical points in linear neural networks, 31st Conference on Neural Information Processing Systems (NIPS), Long Beach, December, 2017 (link)
Attitude estimation with feedback particle filter
The main contribution of this project is to derive the feedback particle filter algorithm for attitude estimation problem. FPF is originally formulated in the Euclidean setting. In this project, we extended the FPF formulation to a very general setting of Riemannian manifolds. In its general form, we showed that the FPF is provides an intrinsic description of the filter that automatically satisfies the geometric constraints of the manifold. Moreover, the particle dynamics retains the feedback structure of the Kalman filter which makes it robust. For the special case when the manifold is a matrix Lie group, we derived explicit formulae for the filter, using the matrix coordinates and quaternions.
- C. Zhang, A. Taghvaei, P. G. Mehta. Feedback Particle Filter on Riemannian Manifolds and Matrix Lie groups, IEEE Transactions on Automatic Control (TAC), Nov, 2017. (link) (pdf)
- C. Zhang, A. Taghvaei, P. G. Mehta. Attitude Estimation of a Wearable
Motion Sensor, IEEE American Control Conference (ACC), Seattle, May, 2017. - C. Zhang, A. Taghvaei, P. G. Mehta. Attitude Estimation with Feedback Particle Filter, IEE Conference on Decision and Control (CDC), Las Vegas, December, 2016. (pdf)
- C. Zhang, A. Taghvaei, P. G. Mehta. Feedback Particle Filter on Matrix Lie group, In Proc. of the 2016 American Control Conference (ACC), Boston, June, 2016. (pdf)
A Coupled Oscillator-based Control Architecture for optimal control of Locomotion
The motivation of this project comes from the problem of sensorimotor control of locomotion. In particular, I worked on the problem of optimal control of locomotory gaits in bio-inspired robots, based on noisy sensor measurements. I presented a bio-inspired central pattern generator (CPG) architecture for optimal maneuvering control of periodic locomotory gaits. The CPG circuit is realized as a coupled oscillator feedback particle filter. The collective dynamics of the filter are used to approximate a posterior distribution that is used to construct the optimal control input. I illustrated the architecture with the aid of a model problem involving locomotion of coupled planar rigid body systems, with two links. For this problem, I designed the coupled oscillator feedback particle filter and demonstrated its control performance in a simulation environment.
- A. Taghvaei, S. A. Hutchinson, and P. G. Mehta. A Coupled Oscillator-based Control Architecture for Locomotory Gaits, IEEE Conference on Decision and Control (CDC), Los Angeles, December 2014 (pdf)

